THE SIMPLEX METHOD
An algebraic technique that applies to any number of variables and enables us to solve larger linear programming problems is called the simplex method.

A linear programming problem may look like:

Maximize: z = 4x1 + 12x2,  subject to

3x1 + x2£ 180
 x1 + 2x2£ 100
-2x1 + 2x2£ 40
x1 ³ 0, x2 ³ 0
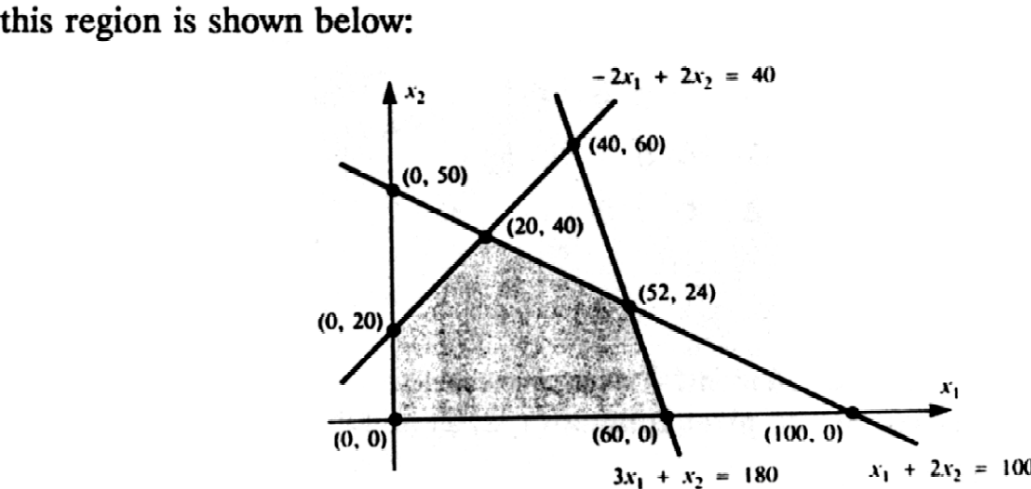
to solve this problem graphically, we graph the feasible region formed by the lines:
3x1 + x2 = 180
x1 + 2x2 = 100
-2x1 + 2x2 = 40
 x1 = 0, x2 = 0



we examine the boundary points: (0, 0), (60, 0), (52, 24), (20, 40), and (0, 20) and substitute these values for x1 and x2 into the equation: z = 4x1 + 12x2
 
Point The value of z
(0, 0) 4(0) + 12(0) = 0 + 0 = 0
(60, 0) 4(60) + 12(0) = 240 + 0 = 240
(52, 24) 4(52) + 12(24) = 208 + 288 = 496
(20, 40) 4(20) + 12(40) = 80 + 480 = 560
(0, 20) 4(0) + 12(20) = 0 + 240 = 240
the maximum value of z is 560 corresponding to the point (20, 40). So our answer is x1 = 20, x2 = 40, and z = 560.

Lets solve the same system using the simplex method:

The first step in the simplex method converts the constraints to linear equations by introducing additional variables called slack variables. The first constraint, 3x1 + x2 £ 180, is true for pairs of numbers such as x1 = 5 and x2 = 17 because 3(5)+17 £ 180. Also note that 3x1 + x2 + 130 = 180 when x1 = 10 and x2 = 20. The 130 in this case 130 is called the slack variable for the first constraint (denoted by s1). The objective function, z = 4x1 + 12x2, can be rewritten as: -4x1 - 12x2 + z = 0

With the addition of slack variables, the constraints become:

                   3x1 + x2 + s1                                   = 180
                    x1 + 2x2        + s2                           = 100
                   -2x1 + 2x2             + s3                    = 40
                   -4x1 - 12x2                    + z              = 0
                    x1 ³ 0, x2 ³ 0, s1 ³ 0, s2 ³ 0, s3 ³ 0
we now form the augmented matrix of this system:
the second step is to find the pivot element. Look at the last row and pick out the most negative entry (-12). This selects the pivot column (1, 2, 2) above.

We need to get the pivot row. Divide each constant (180, 100, 40) by the corresponding entries in the pivot column:
 


Select the smallest ratio (to get the pivot row):

(i)    Ignore all negative ratios.
(ii)   If a zero ratio occurs, then if the zero was obtained by dividing a zero by a negative number
        then ignore the zero.
(iii)  If it was obtained by dividing a zero by a positive number, use that row for the pivot row.

The smallest is 20 determining the pivot row. The pivot element is (2) in the second column third row.

The third step is pivoting, like matrices, make the pivot element a 1 and the rest of the pivot column 0's. So, divide the third row by 2 to get:
 


now we need zeros above and below the pivot element:
 


the forth step: is z maximized?

If the last row contains any negative numbers, z is NOT maximized and we have to repeat steps 2, 3, and 4 again.

We need to find another pivot element. Look at the last row and pick out the most negative entry (-16). This selects the pivot column (4, 3, -1) above.

We need to get the pivot row. Divide each constant (160, 60, 20) by the corresponding entries in the pivot column:
 


The smallest ratio is 20 determining the pivot row. The pivot element is (3) in the first column second row.

Then pivoting, make the pivot element a 1 and the rest of the pivot column 0's. So, divide the second row by 3 to get:
 

and get zeros above and below the pivot element:
 


Is z maximized?

The last row contains no negative numbers so z is maximized.

What is the final answer?

Notice that the first, third and last columns' are unit columns; so the basic variables are x1, x2, s1, and z. The feasible solution is obtained by setting s2 and s3 = 0 and solving for the others:

                   x1=20, x2=40, s1=80, s2=0, s3=0, z=560

Notice also this is the same answer obtained in the first page.

Lets try to solve a Minimization problem:

Minimize:      z = 3x1 + 5x2 + 2x3,  subject to
                    6x1 + 9x2 + 12x3 £ 672
                    x1 - x2 + 2x3 = 92
                    5x1 + 10x2 + 10x3 ³ 480
                    x1 ³ 0, x2 ³ 0, x3 ³ 0
Summary of the Simplex Method for Minimization Problems:
 
1. Maximize w = -z.

2. (³ constraint) For EACH constraint of the form: a1x1 + a2x2 + ... + anxn ³ b,
     multiply the inequality by -1 to obtain: -a1x1 - a2x2 - ... - anxn £ -b.

3. Replace (= constraint) of the form: a1x1 + a2x2 + ... + anxn = b, with two:
     a1x1 + a2x2 + ... + anxn £ b and a1x1 + a2x2 + ... + anxn³ b
     the later is written as: -a1x1 - a2x2 - ... - anxn £ -b

4. Form the initial tableau.

5. If NO negative entry appears in the last column of the initial tableau, proceed to
    Phase II.

6. (Phase I) There is at least one negative entry in the last column:
      (a) The pivot row, the row containing the most negative entry in the last column.
      (b) The pivot column, select the most negative entry in the pivot row (left to
            right).
      (c) Pivoting on the pivot column.

7. Repeat step 6 till you get no negative entries in the last column.

8. (Phase II) Use the standard simplex (maximization procedure) to obtain a solution.
 
To use the simplex method, we modify this problem to the following:
Maximize:    w = -z = -3x1 - 5x2 - 2x3,   subject to
                     6x1 + 9x2 + 12x3 £ 672
               *    x1 - x2 + 2x3 £ 92
               *    x1 - x2 + 2x3 ³ 92
               *    -5x1 - 10x2 - 10x3£ -480
                     x1 ³ 0, x2 ³ 0, x3 ³ 0
Notice the changes in the marked rows (*).

Phase I. The initial tableau is


Pivot on -10 in Row 4, Column 2 to obtain


Pivot on -3 in Row 3 to obtain


Phase II. Pivot on the 1 in Row 2, Column 6 to obtain


The optimal solution is maximum w = -100 at x1 = 0, x2 = 4/3, x3 = 140/3. Thus the original problem has the optimal solution z = -w = 100 at x1 = 0, x2 = 4/3, x3 = 140/3.
 


 
 

Revised: Summer 1999
Student Learning Assistance Center (SLAC)
Southwest Texas State University