The traditional traveling salesman problem involves a salesman who must make a tour through some set of cities. Starting at an arbitrary city, the salesman must visit the other cities and then return to the starting city. The distance between every city pair is specified and the salesman is to visit each city once and only once. A solution is called a tour and the goal is to find the minimum length tour. This problem is considered by the Optimize add-in.

The routing problem addressed by the Combinatorics add-in is similar to the TSP, but here we are dealing with a vehicle that starts at a depot, visit several sites and returns to the depot. The objective is to minimize the travel cost plus a cost that depends on the times of deliveries to the cities. The parameters of the problem are set in the dialog below.

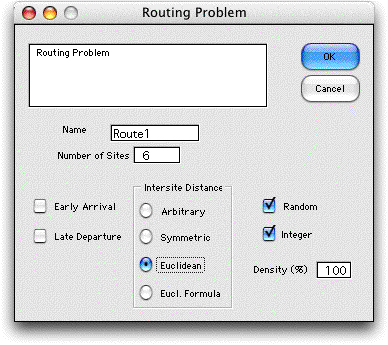
Features of the problem are illustrated by the example. Two additional sites are defined for the analysis. The site indexed 1 represents the depot at the start of the route, the site indexed 8 represents the depot at the end of the route, and the six specified sites are indexed 2 through 7.

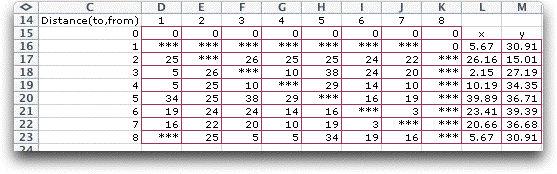
Time is the essence of this problem. A distance matrix (rows 16 to 23) describes the distances between each pair of sites. Note that entry (i, j) holds the distance to site i from site j. This is different than the usual definition, but more convenient for modeling. Since the random, Euclidean and integer options were specified, the locations of the sites are randomly generated and shown in columns L and M. Sites 1 and 8 both represent the depot and they have the same location. The Euclidean distances between the site locations are computed and the integer portions of the values are placed in the table. If the Euclidean Formula option had been chosen, Excel formulas evaluate the distances. The user can then provide non-random locations for the sites in columns L and M. If a density less than 100% is chosen cells are randomly selected to hold a numeric value with the specified probability. The remainder of the cells are made inadmissible by placing the string "***" in them. The add-in assures that at least one feasible tour exists.

Since the tour must start at index 1, all cells allowing a transition from a site other than the last site are disallowed. Similarly all cells representing a transition from the last site to other sites, except the first, are disallowed. Also the cell from 1 to 8 is disallowed. The cell from 8 to 1 completes every feasible tour.

Refer to the figure below for the remainder of the discussion about the example. Distances are translated into costs by cost/distance factors (row 26), and into time by time/distance factors (row 27). The vehicle must spend time at each site, perhaps for loading and unloading, called the site time (row 28). There is also an available time for each site that is the earliest time a site can accept the arriving vehicle. The objective in this problem is to minimize the cost associated with the route. The duration time penalty multiplies the departure time from each site to determine the cost of the tour. Early and late costs may also be included as described later.

The sequence of sites visited by the vehicle is called a tour. The tour begins at the depot and ends at the depot. The initial default tour follows the sites in numerical order as in row 10. The decision variables for the problem specify the next site to visit in row 9 and the tour is computed from these decisions. Row 12 shows the travel distance from a site to the next site in the tour.

Immediately below the data, the sequence is evaluated. We see in row 32 the titles of the sites in the order visited and row 33 shows the numerical indices of the sites. Row 34 shows the time the site is available to accept the arriving vehicle. Lines 36 and 37 hold the processing time at the sites and the travel times to the next site. The travel times are computed by multiplying row 12 (travel distance) by row 27 (time/distance).

Based on these numbers the arrival and departure times at the sites are computed in lines 38 and 39. The arrival time at a site is the departure time from the previous site plus the travel time between the sites. The departure time for a site is the arrival time plus the site time.

The costs for traveling to the next site are computed in row 42 by multiplying the contents of rows 12 (travel distance) and 26 (cost/distance). The duration costs are computed in row 43 by multiplying row 39 (departure times) by row 30 (departure time penalty). The goal is to minimize the total of the travel costs and duration costs.

We choose a solution method by clicking the Search button on the worksheet. The button calls a dialog from the Optimize add-in for selecting the solution method. The figure below shows the worksheet with the optimum solution found with exhaustive enumeration. The cells defining the optimum tour are outlined in red on the distance matrix.

The tour results begin in row 32 with the optimum sequence of site visits with the computed arrival and departure times. The costs for the tour begin on row 42. Below the results we show part of the Gantt chart. Travel times are shown in black and site times are colored. Only sites with nonzero site times are shown in the chart. We use a site time of 1 at both the starting and ending depot sites so that the white depot cells identify the beginning and end of the chart.

The list below shows the best 19 solutions found by exhaustive enumeration. The optimum solution was also found by generating 10 random tours and improving each with a 2-change heuristic. Of course, such a fortuitous result cannot be guaranteed.

Scheduled Arrival and Departure Times

To include scheduled arrivals and departures in the data, click the Early Arrival and Late Departure checkboxes. For this example, we construct the distance matrix with formulas determining the Euclidean distances.

The form for the example is shown below with data. The solution is the optimum sequence. The data assumes that the vehicle is to finish its route before 240 minutes or 4 hours. Sites 1, 2 and 3 have been promised that the departure times will be no later than 120 minutes. Sites 4, 5 and 6 have been promised that the vehicle will arrive no earlier than 120 minutes and that departure will be no later than 240 minutes. To encourage a completion time for the entire route of 240 minutes, we have placed 240 as the scheduled departure from the final depot site. Scheduled arrivals and departures are soft constraints. We encourage them to be satisfied by penalizing arrivals that come before the scheduled times and departures that occur after the scheduled times. A greater penalty is applied to the last depot site to give greater priority to the desired tour completion time. The data also specifies that site 2 will be available no earlier than 10 and site 3 will be available no earlier than 55. These are hard constraints.

The optimum sequence has site 2 (index 3) as the first site on the route. The vehicle arrives at time 10, when the site is first available. This is 30 minutes before the schedule arrival resulting in a penalty of 600. The second site on the tour, S3, is within the scheduled time window. The departure time for S1 is 4 minutes after the scheduled departure time resulting in a penalty of 80. The entire tour is finished at 231 minutes, within the desired limit.

The chart of the solution shows that the vehicle is idle before traveling to S2 and before traveling to S3. These idle stretches are caused by the time available restrictions. With no such restrictions the vehicle will never be idle. The formulas defining the arrival and departure times assume that unless restricted by times available, the vehicle is never delayed. This may not be a correct assumption with nonzero early scheduled arrivals when it may be advisable to delay the vehicle so that it does not arrive too early. This option is not considered by the add-in.

Clicking the Map button on the page (the button is added in later versions) causes a worksheet to be created that shows the solution graphically. Note that the route is different than the example without early and late times.