-Markowitz Portfolio

Harry Markowitz presented a theory for selecting financial securities for an investment portfolio in the paper "Portfolio Selection", in the Journal of Finance, Vol. VII, No. 1, March 1952. The paper is widely referenced. Two generally conflicting measures evaluate the portfolio, the expected return and the variance of the return. The latter represents the risk of the portfolio. The investor desires a portfolio that has a high return and low risk. Since the goals of maximizing return and minimizing risk are usually conflicting, we create a model that minimizes variance while satisfying a constraint on the return. By solving the model for a series of returns we obtain an efficient frontier of solutions. Depending on the investor's risk tolerance, he or she should choose one of these solutions Markowitz computes the variance of a portfolio using the Covariance matrix.

The Portfolio add-in creates the structure to hold historical data, constructs a mathematical programming model, provides for solving the model and provides for generating the efficient frontier.

The Math Programming add-in constructs the math programming model and the Solver add-in solves the model, so those two add-ins must be installed in addition to the Portfolio add-in. Before attempting to create a model, choose the Solver command from the Tools menu. This opens the Solver dialog. Then immediately close the dialog. This establishes contact with the Solver. This step must be performed every time Excel is launched.

To create a model choose Markowitz from the Portfolio menu. The dialog below is presented to set the size parameters for the problem. We choose an example with eight securities with 24 periods of data. The model will minimize variance subject to a constraint on return. Alternatively, we could maximize return subject to a constraint on variance. The Frontier analysis is only available with the minimize variance option. When selected the Make Random Problem option provides data that is randomly generated, but realistic.

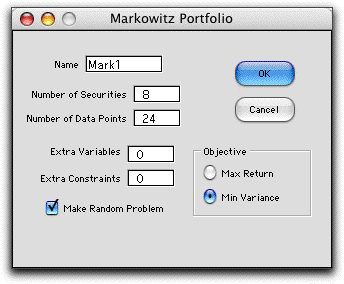
The Extra Variables and Extra Constraints boxes allow the creation of a larger math programming model for more complex problems.

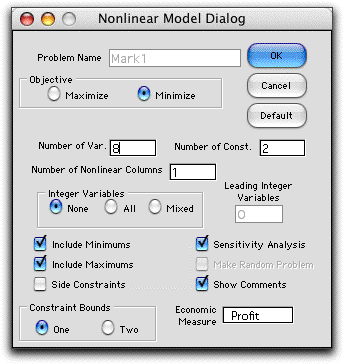
The next dialog that appears is from the Math Programming add-in. It specifies the creation of a nonlinear programming model. Some of the information on the dialog may not seem correct but the add-in changes the model after it is placed on the worksheet. Although it is possible for the user to change some of the items on this dialog, it best to accept all the data as presented.

Worksheet

The add-in creates a new worksheet with the name specified in the Portfolio dialog. Since there is quite a bit of information on the sheet, we describe the sheet from the bottom up.

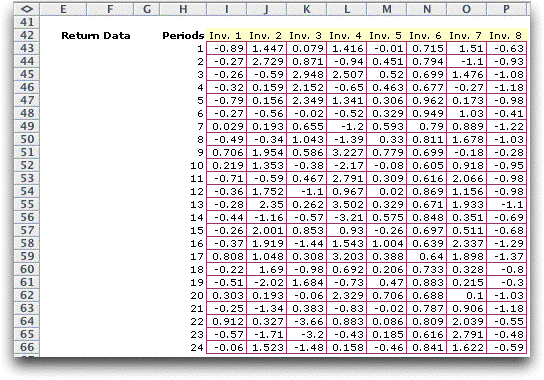
The first information presented are the rows for data. A randomly generated example is shown with 24 periods of data. The interval of the period depends on the frequency of portfolio changes envisioned and the availability of data. For a long-term investor, a one month period would seem reasonable. The data describes the returns for the periods measured as percentages. The first item, –0.89, would indicate a decline of 0.89% in the value of the associated security.

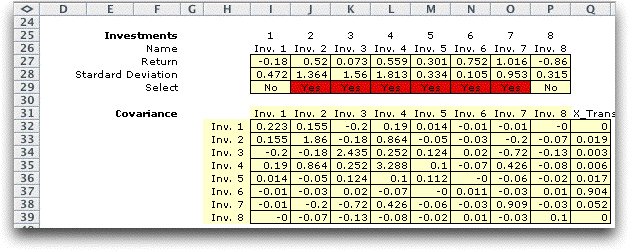
Immediately above the data is the statistical analysis necessary for the Markowitz model. Row 26 holds the security names. These can be set by the analyst and they will be reflected throughout the worksheet. Row 27 computes the average value for each data column and row 28 computes the standard deviation. Row 30 indicates with a red field the securities that have nonzero values in the portfolio. The matrix in the range I32:P39 is the covariance matrix. The main diagonal holds the variances of the securities.

The statistical analysis is entirely computed with Excel built-in functions. Some representative cell formulas are shown below. The name in the formulas (Mark1_Return1) refers to data cells in the range I43:I66. Cells on the main diagonal are computed with the VAR function. Cells above the diagonal are computed with the COVAR function and cells below the diagonal equal the corresponding values above the diagonal.

The covariance matrix is always symmetric and has the positive definite characteristic. This guarantees that the variance objective is strictly convex and that there is a single local minimum point that is also the global minimum. This simplifies the problem of finding the optimum solution.

The math programming model is at the top of the worksheet. A mathematical statement is given later on this page. The result shown below is the minimum variance solution when the return is required to be at least 0.75. This value is entered in cell L21. All yellow areas in the model hold formulas and should not be changed by the user. Cell H13 computes the variance of the portfolio using matrix computations. Row 17 holds the constraint that the portfolio proportions must sum to 1. Row 18 holds the constraint that the average return be at least 0.75.

This is a nonlinear minimization problem with a convex objective function and linear constraints. With these conditions there should be a unique local minimum (if there is a feasible solution). The Excel Solver will sometimes report that there is no feasible solution when there actually is one. We have found that setting the initial proportions to 1/n in the green array of Row 8 often leads to a feasible solution.

As suggested by Markowitz, the optimum solution will often be diversified with several securities included in the portfolio. This is also suggested by the nonlinear-strictly convex nature of the objective function. For the example, investment 6 with the greatest return comprises 90% of the portfolio with five other securities completing the portfolio. We will see that the character of the solution changes with the value chosen for the minimum return.

Efficient Frontier

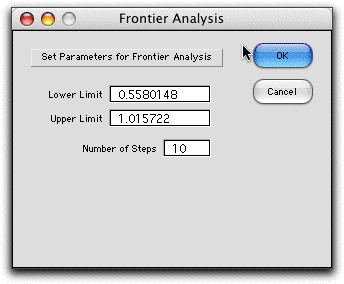
Clicking the Frontier button on the worksheet initiates the process of finding the efficient frontier. The add-in sets the lower bound on the return to zero and solves the model. The result is the minimum variance solution. The corresponding value of the portfolio is used as the lower limit on the frontier. The upper limit on the return value is the largest return from the available securities. If this security is selected as the sole component of the portfolio the highest portfolio return is obtained. This return is used as the upper limit. Both limits may be changed if the analyst would like to investigate a narrower range. The number of steps in the analysis is provided by the entry in the third field.

The range of returns is divided into the specified number of intervals and the model is solved for the interval boundaries. There will be one more solution than the number of steps. The results are shown in the table below for the example. Only feasible solutions are included in the table.

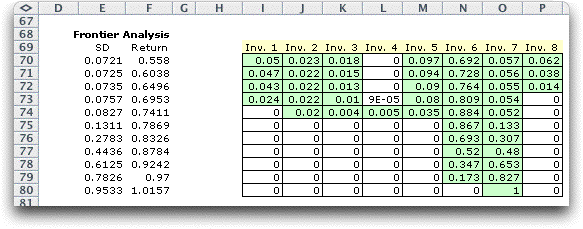
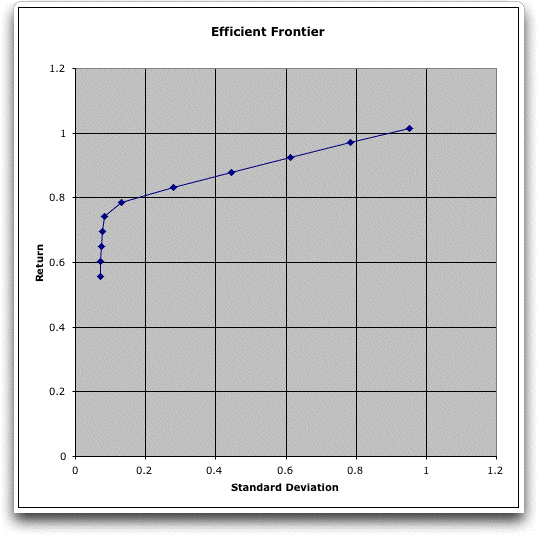
The minimum variance solution (as indicated by the standard deviation column) uses seven securities and has the maximum diversity. As the minimum return is increased, the resultant solutions have increased variance and are generally less diverse. The final solution uses only security 7. The chart of the frontier, placed below the table on the worksheet, shows that the portfolio return initially sharply increases as the variance is increased only slightly. After about 0.7, higher returns can only be obtained with significantly increased variability.

The efficient frontier for the Markowitz portfolio consists of a continuum of solutions and the frontier will be a strictly concave function. We only find a finite number of solutions and connect adjacent solutions by straight lines on the chart. The actual frontier will have solutions slightly above the lines. A more accurate frontier can be found by using more steps in the analysis.

The variance of the portfolio can be computed from the Covariance matrix as shown below.

We use statistical estimates from the historical data to compute the Covariance matrix used by the model.

The math programming model limits the total return while requiring that the security proportions sum to 1. The goal is to minimize portfolio variance.

The model may also be constructed to maximize return with a constraint on the variance. Since this model has a linear objective function with a nonlinear constraint, the problem is somewhat more difficult to solve than the minimum variance model.

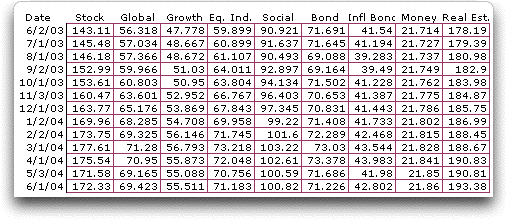
To illustrate data taken from reality, we obtained the monthly unit values for the asset funds of the CREF annuity investment account. The data for one year is shown below.

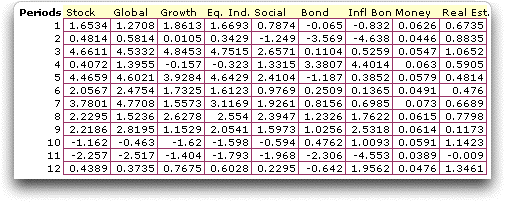
We compute the monthly return for each fund with the formula:

100*(BV - EV)/BV

BV is the unit value at the beginning of the month, EV is the value at the end of the month. We multiply by 100 to express the returns as percentages. The resultant table of returns is below.

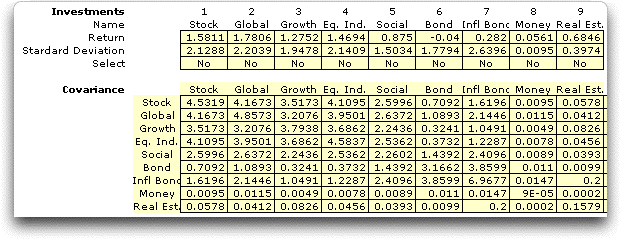
Statistical analysis computes the following averages, standard deviations and covariance matrix. Note that all the covariances are positive in this case.

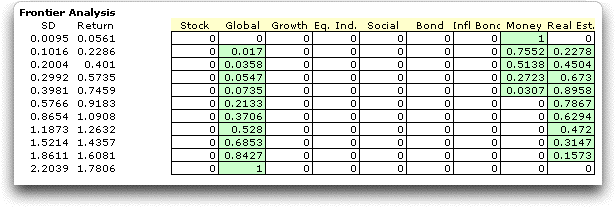
Solutions on the efficient frontier with ten steps are found using the add-in.

The corresponding efficient frontier is in the graph below.

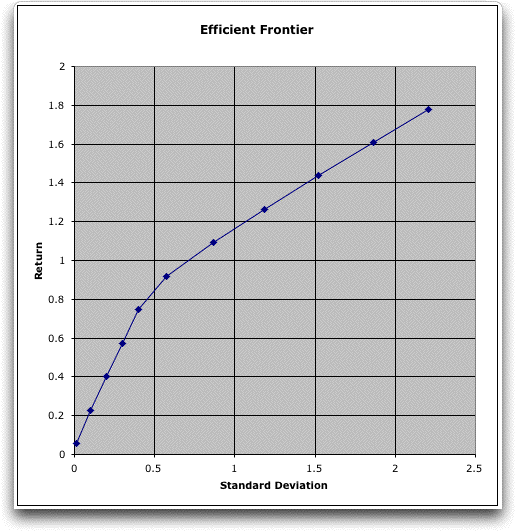
The minimum variance portfolio uses only the Money Market investment. The maximum return (with maximum variance) invests in only the Global Equities. Intermediate solutions use a combination of Money Market, Real Estate and Global Equities. The portfolio for a specific investor depends on his or her risk preference. Our example uses only one year of data. The results would probably change if a longer history were used.