Artificial-variable Free Solution
Algorithms for LP Models



Europe Mirror Site
Mirror Site for Asia
Mirror Site for Middle East
USA Site


It is easy to create general but hard-to-use solution algorithms, and it is easy to create easy-to-use but specialized solution algorithms. It's really good to make a solution algorithm that is both general and easy to use.
Professor Hossein Arsham   

To search the site, try Edit | Find in page [Ctrl + f]. Enter a word or phrase in the dialogue box, e.g. "parameter " or "linear " If the first appearance of the word/phrase is not what you are looking for, try Find Next.

   MENU

   Companion Sites:

Introduction

The Algebraic Method presented earlier, has a major deficiency in that it results in all corner points including the infeasible one which must be discarded. The simplex method is an efficient implementation of the algebraic method. However, the best known complexity result belongs to the primal dual path-following infeasible interior point methods with an iteration count of O(sqrt(n)L) to obtain an approximate solution from which the true solution can be obtained directly. Here L is the so called information length (binary coding length of input). However, the implementation of various interior point methods requires an stating point, and it has been shown that the performances of these algorithms are, unfortunately, tremendously influenced by the starting point. That is way, the simplex method still is the best algorithm that also provides useful post-optimal information for the decision makers.

The presentation of the simplex method, which solves linear programming (LP) problems, is not universal. In the U.S.A. instructors on the West coast enjoy solving the minimization problems, while in the East the maximization version is preferred. Even within each of these groups you will find differences in presenting the simplex rules.

The two popular approaches being taught are the primal simplex method (PS) and the dual simplex method (DS). In the PS, the initial tableau has a complete basic variable set and a non-negative RHS column. This method strives to make the last row non-positive at which point the final tableau has been achieved. In the DS, the basic variable set is also complete in the initial tableau, the last row is non-positive, and the method strives to makes the RHS non- negative.

The PS may require the use of artificial variables while the DS may require artificial constraint. These two methods are traditionally discussed in classrooms and are described more fully in traditional LP textbooks. What is novel in the artificial-free approaches is that the only requirement for the initial tableau is that the RHS is non- negative.

When one tries to solve any given problem by any of several standard phase I approaches, one becomes quickly convinced of the simplicity of the artificial-free method. Moreover, there is adequate testimony from many instructors as to the ease of insights of the concept of artificial variables or artificial constraints or artificial objective functions for business and industrial students with limited mathematical background. Precisely because these mechanisms are artificial, they lack relevance to the underlying real-world LP problem.

We present three different solution algorithms to solve any type of LP problems. All techniques are based on some extensions of the algebraic method. Before you start, put the linear program into standard form. This means making the linear program the maximization, with RHS non-negative, and changing inequality constraints (except the non-negativity conditions) to equality constraints by introducing slack/surplus variables.

The first two solution algorithms start with has no basic variables in the initial tableau. Therefore, these approaches may well provoke uneasiness and indeed disbelief among those practitioners schooled in the traditional methods which defines a simplex tableau as having a complete basic variable set. It is in this difference that the artificial-free offers a contribution to the literature.

All variables must be non-negative: Convert any unrestricted variable Xj to two non-negative variable by substituting y - Xj for every Xj everywhere. This increase the dimensionality of the problem by one only (introduce one y variable) irrespective of how many variables are unrestricted. If there are any equality constraints, one may eliminate the unrestricted variable(s) by using these equality constraints. This reduces dimensionality in both number of constraints as well as number of variables. If there is no unrestricted variables do not remove the equality constraints by substitution, this may create infeasibility. If any Xj variable is restricted to be non-positive, substitute - Xj for Xj everywhere.

The following sites enable you to practice the LP pivoting without having to do the arithmetic!
The Pivot Tool , tutOR, The Simplex Place, Simplex Machine, and LP-Explorer.

Further Readings:

Maros I., Computational Techniques of the Simplex Method, Kluwer Publishers, 2002.

Initialization of the Simplex Method

The main idea in this solution algorithm is that the basic variable set (BVS) does not start out complete in the initial tableau, rather variables are brought in based on their contribution to the objective function value.

To start the algorithm the LP problem must be converted into the following standard form:

  1. Must be a maximization problem,
  2. RHS must be non-negative,
  3. All variables must be non-negative,
  4. Convert all inequality constraints (except the non-negativity conditions) into equalities by introducing slack/surplus variables.

Detailed Process:

Step 1. Construct the initial tableau which is always considered to have empty BVS (do not occupy any row with any variable including slack variables).

BVSet Augmentation Phase:

General Strategy: Push toward optimal solution (if it exists) while maintaining feasibility. The problem is infeasible if the push towards all directions are infeasible.

Step 2. Is the BVS complete? If yes Go To Phase 2, Otherwise continue

Step 3. Pivot Column: A candidate to enter into the BVS is a non-basic variable with largest Cj (could be negative). If there are ties choose the first one from the left side. Continue

Step 4. Compute C/R (i.e. RHS/PC), Does the smallest non-negative C/R belong to an unoccupied row? If yes
Pivot Row: Enter the variable into BVS by performing the GJ row operations, and return to Step 2. If Not Go To Step 5

Step 5. Is there any other non-basic variable as candidate to enter? If yes the next variable with the largest Cj and Go to Step 4. Otherwise go to previous tableaux and try other possibilities. If all possibilities are exhausted then the problem is infeasible.

Optimality (Simplex) Phase:

General Strategy: Move from corner point to a better corner point in the search of optimal corner point (or the problem is unbounded).

Step 6. Are all Cj non-positive in the current tableau? If yes, go to Step 8; Otherwise continue.

Step 7. Apply the (ordinary) simplex method rules for entering and exiting variables to and from BVS). Go to 6.

Step 8. This is an optimal tableau. Find out all multiple solutions (if the number of Cj = 0 is larger than the size of the BVS) if they exist.

Notes: We make no claim as to computational performance. Nor do we have a pretense that our method always permits solutions in m (the number of constraints) iterations without trying all other possibilities before declaring infeasibility. An algorithm with such performance would indeed be remarkable. At this time the intent is solely to provide an efficient and effective tool for students to do LP by hand-computation without cumbersome inventions

Numerical Examples

The following sites enable you to practice the LP pivoting without having to do the arithmetic!
The Pivot Tool , tutOR, The Simplex Place, Simplex Machine, and LP-Explorer.

Example 1: The following problem is attributed to Gert Tijssen.

Max -X1 - 4X2 - 2X3,
subject to:
X1 - X2 + X3 = 0,
-X2 + 4X3 = 1,
and X1, X2, X3 ³ 0.

Since the constraints are already in equality form, the initial tableau is readily available for this problem:

BVS X1 X2 X3 RHS C/R
?(1)-1100/1
?0-1 41 --
Cj-1-4-2

By Step 3, the candidate variable to enter is X1 and by Step 4 the smallest C/R belongs to an open row, so its position is the first row. After pivoting we get:

BVS X1 X2 X3 RHS C/R
X11-110 --
? 0-14 11/4
Cj0-5-1

The next candidate variable to enter is X3, performing GJ pivoting the RHS(1) becomes negative. Therefore, we should try X2. The C/R is negative. As indicated in Step 5, we go back to step 2 to try other candidates.

Consider the previous tableau, instead of bringing X1 in we try the next candidate, which is X3:

BVS X1 X2 X3 RHS C/R
?1-1(1)0 0/1
? 0-1411/4
Cj-1-4-2

Its location is the first row, after performing the GJ operations, we have:

BVS X1 X2 X3 RHS C/R
X31-110--
?-43 01/3
Cj1-60

The candidate variable to enter is X1, however its C/R is negative. Therefore, we pick the next candidate, which is X2. Bringing X2 into BVS, we have:

BVS X1 X2 X3 RHS
X3-1/3011/3
X2-4/3101/3
Cj-700

This is the end of phase 1. The tableau is already optimal. There is no need for phase 2. The optimal solution is: X1 = 0, X2 = 1/3, X3 = 1/3, with the optimal value of -2.

Example 2: The following problem is attributed to Andreas Enge, and Peter Huhn.

Maximize 3X1 + X2 - 4X3
subject to:
X1 + X2 - X3 =1,
X2 ³ 2,
X1 ³ 0

After adding a surplus variable, the initial tableau is:

BVS X1 X2 X3 S1 RHS
?11-101
?010-12
Cj31-40

Bringing X1 into bases we have:

BVS X1 X2 X3 S1 RHS
X111-101
?010-12
Cj0-2-10

Now we cannot bring any variables in while maintaining feasibility. However before declaring infeasibility for the problem we must try other possibilities. Going back to the tableau just before the current one, we try to bring in X2:

BVS X1 X2 X3 S1 RHS
X211-101
? -101-11
Cj20-30

X1 , and S1 cannot come in since they make some RHS values negative. The next variables to come in is X3. The next tableau is the final one.

BVS X1 X2 X3 S1 RHS
X2010-12
X3-1 01-11
Cj-100-3

The optimal solution is X1 = 0, X2 = 2, X3 = 1, with S1= 0.

Example 3: The following problem is attributed to Richard Cottle, Jong-Shi Pang, Richard Stone of Burnsville, Minnesota, and Crnig Tovey.

Maximize 2X1 + 3X2 - 6X3
subject to:
X1 + 3X2 + 2X3 £ 3,
- 2X2 + X3 £ 1
X1 - X2 + X3 = 2
2X1 + 2X2 - 3X3 = 0
X1 , X2 , X3 ³ 0

The initial tableau is:

BVS X1 X2 X3 S1 S2 RHS
?1321 03
?0-21011
? 1-110 02
?22-30 00
Cj23-60 0

Bringing X2 into BVS gives an infeasible sign after one iteration. Therefore we try to bring in X1:

BVS X1 X2 X3 S1 S2 RHS
?027/21 03
?0-21011
? 0-25/20 02
X111-3/20 00
Cj01-300

X2 cannot come in since it makes some RHS negative. The next variables to come in are S1 and S2 without any GJ iterations.

BVS X1 X2 X3 S1 S2 RHS
S1027/21 03
S20-21011
?0-25/20 02
X111-3/20 00
Cj01-30 0

Therefore we try to bring in X3. The next tableau is the final one.

BVS X1 X2 X3 S1 S2 RHS
S1024/501 01/5
S20-6/50011/5
X30-4/510 04/5
X11-1/50006/5
Cj0-7/5000

This is the end of phase 1. The tableau is already optimal. There is no need for phase 2. The optimal solution for decision variables are: X1 = 6/5, X2 = 0, X3 = 4/5.

Example 4: Consider the following problem:

Max -X1 + 2X2
subject to:
X1 + X2 ³ 2,
-X1 + X2 ³ 1,
X2 £ 3,
and X1, X2 ³ 0.

Converting the constraints into equality form, we have:

X1 + X2 - S1 = 2,
-X1 + X2 - S2 = 1,
X2 + S3 = 3

The initial tableau for this problem is:

BVS X1 X2 S1 S2 S3 RHS C/R
?11-10022/1
?-1(1)0-1011/1
?0100133/1
Cj-12000

Although S3 could be considered as a BV, but as always we start phase 1 with an empty BVS. By Step 3 of the algorithm, the candidate variable to enter is X2 and by Step 4 the smallest C/R belongs to an open row, so its position is the second row. After pivoting we get:

BVS X1 X2 S1 S2 S3 RHS C/R
?20-1(1)011/1
X2-110-101--
?100112 2/1
Cj10020

The next variable to enter is S2, which is the slack/surplus of an occupied row namely the second row. Performing GJ pivoting we get:

BVS X1 X2 S1 S2 S3 RHS C/R
S220-1101--
X211-1002--
?-10(1)0111/1
Cj-30200

The next incoming variable is S1, generating the next tableau, we obtain:

BVS X1 X2 S1 S2 S3 RHS C/R
S2100112
X2010013
S1-101011
Cj-100-2

This is the end of phase 1. The tableau is already optimal. There is no need for phase 2. The optimal solution for decision variables are: X1 = 0, X2 = 3 with the optimal value, which is found by plugging the optimal decision into the original objective function, we get the optimal value = 6.

Example 5: Consider the following problem:

Max 6X1 + 2X2
Subject to: 2X1 + 4X2 £ 20, 3X1 + 5X2 ³ 15, X1 ³3, X2³ 0.

The Initial tableau:

BVS X1 X2 S1 S2 S3 RHS C/R
S12410020---
?350-1 01515/3 = 5
?1000 -133/1 = 3
Cj62000

X1 enters into the BVS. First tableau is:

BVS X1 X2 S1 S2 S3 RHS C/R
S10410214--
?050-1366/3 = 2
X11000 -13--
Cj02006

Now S3 enters. The second tableau is:

BVS X1 X2 S1 S2 S3 RHS C/R
S102/312/301010/(2/3) =15
S305/30-1/312--
X115/30-1/305--
Cj0-8020

The BVS is complete. Start the ordinary Simplex method.

BVS X1 X2 S1 S2 S3 RHS
S2013/21 015
S3021/2017
X1121/20010
Cj0-10-300

This is the final tableau, which provides all the following information. The optimal solution is X = 10, X = 0. The slack and surpluses are S = 0, S = 15, S = 7. The solution to the dual problems are: U = 3, U = 0, and U = 0.

Example 6: Solve the following problem:

Consider the following problem:

Max 3X1 + 5X2,
subject to:
2X1 + X2 = 10,
X1, and X2 ³ 0.

Since the constraint is already in equality form, the initial tableau is readily available for this problem:

BVS X1 X2 RHS
?2(1)10
Cj35

By Step 3, the candidate variable to enter is X2 and there is only one open row, so its position is the first row. After pivoting we get:

BVS X1 X2 RHS
X22110
Cj-70

This is the end of phase 1. The tableau is already optimal. There is no need for phase 2. The optimal solution is: X1 = 0, X2 = 10, with the optimal value of 50.

Now the question is: How to compute the shadow price? The dual problem is

Min 10U1
subject to:
2U1 £ 3,
U1 £ 5,
and U1 is unrestricted in sign.

Since X2 in not zero, the second constraint in the dual problem must be binding (by the complementary slackness theorem). This gives the solution to the dual problem as U1 = 5, with the same optimal value = 50 as expected. Therefore, the shadow price for the RHS of the primal problem is equal to 5.

Example 7: By default, in this solution algorithm just like almost all LP solvers (such as LINDO), we assumed that all variables are non-negative.

To achieve this requirement, convert any unrestricted variable Xj to two non-negative variable by substituting y - Xj for every Xj everywhere. This increases the dimensionality of the problem by one only (introduce one y variable) irrespective of how many variables are unrestricted.

If any Xj variable is restricted to be non-positive, substitute - Xj for Xj everywhere. This reduces the complexity of the problem.

Solve the converted problem, and then substitute back to get the values for the original variables.

The following numerical example illustrates the process:

Maximize -X1
subject to:
X1 + X2 ³ 0,
X1 + 3X2 £ 3.

The converted problem is:
Maximize -y + X1
subject to:
-X1 - X2 + 2y ³ 0,
-X1 - 3X2 + 4y £ 3,
X1 ³ 0,
X2 ³ 0,
and y ³ 0.

BVS X1 X2 y S1 S2 RHS C/R
? -1-12-1000/2
? -1-340133/3
Cj10-100

The first variable to come in is X1:

BVS X1 X2 y S1 S2 RHS C/R
X111 -2100--
?0-221133/2
Cj0-11-10

The next variable to come in is y:

BVS X1 X2 y S1 S2 RHS
X11-10213
y0-111/2 1/23/2
Cj000-3/2 -1/2

The optimal solution for the original variables is: X1 = 3/2 - 3 = -3/2, X2 = 3/2 - 0 = 3/2, with optimal value of 3/2.

Is there any other optimal solutions? Notice that the number of zeros in the last row of the final tableau exceeds the number of basic variables (this is the necessary condition for the existence of multiple solutions), however, one cannot bring in X2 into the basic variable set. Therefore, this solution is the only optimal solution.

Further Readings:

Arsham H., Initialization of the simplex algorithm: An artificial-free approach, SIAM Review, Vol. 39, No. 4, 736-744, 1997.
Arsham H., An artificial-free simplex algorithm for general LP models, Mathematical and Computer Modelling, Vol. 25, No. 1, 107-123, 1997.

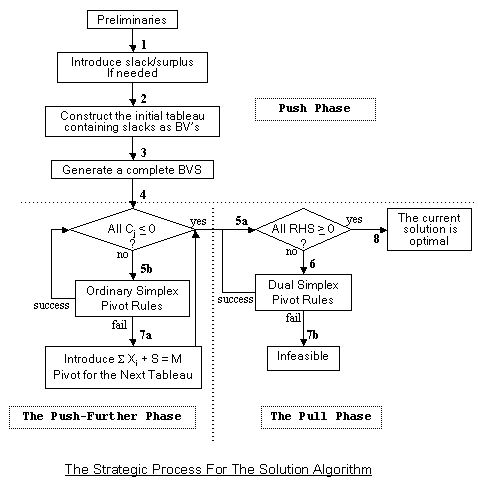
The Push-to-Pull Solution Algorithm

The second solution algorithm is artificial-variable free. The algorithm consists of preliminaries for setting up the initialization followed by three main phases: Push, Push Further, and Pull phases. The Push Phase develops a basic variable set (BVS), which may or may not be feasible. Unlike simplex and dual simplex, this approach starts with an incomplete BVS initially, and then variables are brought into the basis one by one. If the BVS is complete, but the optimality condition is not satisfied, then Push Further Phase pushes until this condition is satisfied. This strategy pushes towards an optimal solution. Since some solutions generated may be infeasible, the next step, if needed, the Pull Phase pulls the solution back to feasibility. The Push Further Phase satisfies the optimality condition, and the Pull Phase obtains a feasible and optimal basis. All phases use the usual Gauss pivoting row operation.

The initial tableau may be empty, partially empty, or contain a full basic variable set (BVS). The proposed scheme consists of the following three strategic phases:

Push Fill-up the BVS completely by pushing it toward the optimal corner point, while trying to maintain feasibility.

Push Further If the BVS is complete, but the optimality condition is not satisfied, then push further until this condition is satisfied.

Pull If pushed too far in Phase I, pull back toward the optimal corner point (if any). If the BVS is complete, and the optimality condition is satisfied but infeasible, then pull back to the optimal corner point; i.e., a dual simplex approach.

Not all LP problems must go through the Push, Push Further and Pull sequence of steps, as shown in the numerical examples.

To start the algorithm the LP problem must be converted into the following standard form:

  1. Must be a maximization problem
  2. RHS must be non-negative
  3. All variables must be non-negative
  4. Convert all inequality constraints (except the non-negativity conditions) into equalities by introducing slack/surplus variables.

The following three phases describe how the algorithm works. It terminates successfully for any type of LP problems since there is no loop-back between the phases.

The Push Phase:

Step 1. By introducing slack or surplus variables convert all inequalities (except non-negativity) constraints into equalities. The coefficient matrix must have full row rank, since otherwise either no solution exists or there are redundant equations.

Step 2. Construct the initial tableau containing all slack variables as basic variables.

Step 3. Generate a basic variable (BV) set, not necessarily feasible, as follow:

  1. Incoming variable is Xj with the largest Cj (the coefficient of Xj in the objective function, it could be negative), and if possible with smallest non-negative C/R. Otherwise try the next variable to enter. If there are alternatives, break the ties arbitrarily.

  2. Is Xj the last variable to enter into BV set? If yes, enter it into the empty row and generate the next tableau (if impossible to pivot, go to Step 3(1) and choose the next Cj) and go to Step 4. Otherwise its row position is the row having the smallest non-negative C/R. Do not consider the rows, which are already occupied. If there are alternative, break the ties arbitrarily.

    Generate the next tableau and go to Step 3(1). If there is no positive C/R, then select the row having smallest non-negative C/R.

The Push Further Phase:

Step 4. Are all Cj £ 0 in the current tableau? If yes, go to Step 5a; otherwise go to Step 5b.

Step 5a. Are all RHS ³ 0 in the current tableau? If yes, go to Step 8. Otherwise go to Step 6.

Step 5b. Use the ordinary simplex pivoting rule:

  1. Identify incoming variable (having largest Cj).

  2. Identify outgoing variable (with the smallest non-negative C/R). If none, unbounded solution. (If more than one choose any one, this may be the sign of degeneracy.) Generate the next tableau and go to Step 4. If Step 5b fails, then go to step 7a.

Step 7a If all RHS ³ 0 , then the optimal solution is unbounded. Otherwise , introduce a new constraint SXi + S = M to the current tableau, with S as a basic variable. Where M is an unspecified sufficiently, large positive number, and Xi's are variables with a positive Cj in the current tableau. Enter the variable with largest Cj and exit S. Generate the next tableau, (this makes all Cj £ 0), then go to Step 5a.

The Pull Phase

Step 6. Use the dual simplex pivoting rules to identify the outgoing variable (smallest RHS). Identify the incoming variable having negative coefficient in the pivot row in the current tableau, if there are alternatives choose the one with the smallest positive row ratio (R/R), [that is, a new row with elements: row Cj/pivot row]; if otherwise generate the next tableau and to Step 5a. If Step 6 fails, then go to Step 7b.

Step 7b. The problem is infeasible. Stop.

Step 8. This is the optimal solution, which could be unbounded. Find out all multiple solutions if they exist (the if the number of Cj = 0 is larger than the size of the BV set, this is a necessary condition).

The algorithmic strategic process is presented in the following flowchart.

Notes:

1. By following Steps 3(1) and 3(2) a complete BV set can always be generated, which may not be feasible. Proof of the first part of this statement follows by contradiction (from the fact that there is no redundancy/inconsistency among the constraints). The second part indicates that by pushing toward the optimal corner point we may have passed it.

2. Note that if all elements in any row are zero, we have one of two special cases. If the RHS element is non-zero then the problem is infeasible. If the RHS is zero this row represents a redundant constraint. Delete this row and proceed.

3. If you ever reach to the Step 7a or 7b, you must go back and check the formulation of the problem, since the problem could be unbounded.

Numerical Examples:

The following sites enable you to practice the LP pivoting without having to do the arithmetic!
The Pivot Tool , tutOR, The Simplex Place, Simplex Machine, and LP-Explorer .

Example 1: The following problem is attributed to Gert Tijssen.

Max -X1 - 4X2 - 2X3,
subject to:
X1 - X2 + X3 = 0,
-X2 + 4X3 = 1,
and X1, X2, X3 ³ 0.

Since the constraints are already in equality form, the initial tableau is readily available for this problem:

BVS X1 X2 X3 RHS C/R
?(1)-110 0/1
?0-141--
Cj-1-4-2

The Push Phase: The candidate variable to enter is X1 and the smallest C/R belongs to an open row, so its position is the first row. After pivoting we get:

BVS X1 X2 X3 RHS C/R
X11-110 --
?0-1(4)11/4
Cj0-5-1

The next candidate variable to enter is X3, performing GJ we have:

BVS X1 X2 X3 RHS
X11-3/40-1/4
X30-1/411/4
Cj0-21/40
R/R-21/3-

Push Further Phase: There is no need for this phase since all Cj's are non-positive.

The Pull Phase: The variable to go out is X1. By row-ratio criterion, the variable to come is X2. After performing the GJ operations, we have:

BVS X1 X2 X3 RHS
X2-1/3011/3
X3-4/3101/3
Cj-700

This tableau is the optimal one. The optimal solution is : X1 = 0, X2 = 1/3, X3 = 1/3. With the optimal value, which is found by plugging the optimal decision into the original objective function, we get the optimal value = -2.

Example 2: The following problem is attributed to Andreas Enge, and Peter Huhn.

Maximize 3X1 + X2 - 4X3
subject to:
X1 + X2 - X3 =1,
X2 ³ 2,
X1 ³ 0

After adding a surplus variable, the initial tableau is:

BVS X1 X2 X3 S1 RHS
?11-101
?010-12
Cj31-40

The Push Phase: Bringing X1 into bases we have:

BVS X1 X2 X3 S1 RHS
X111-101
?010-12
Cj0-2-10

Now bring S1 into BVS:

BVS X1 X2 X3 S1 RHS
X111-101
S10-101 -2
Cj0-2-10
R/R--2----

Push Further Phase: There is no need for this phase since all Cj's are non-positive.

The Pull Phase: S1 goes out and X3 comes in:

BVS X1 X2 X3 S1 RHS
X110-11 -1
X2010-12
Cj00-1-2
R/R----12

The Pull Phase: X1 goes out and X3 comes in.

BVS X1 X2 X3 S1 RHS
X3-101-11
X2010-12
Cj-100-3

This tableau is optimal. The optimal solution is X1 = 0, X2 = 2, X3 = 1, with S1= 0.

Example 3: The following problem is attributed to Richard Cottle, Jong-Shi Pang, Richard Stone, and Crnig Tovey.

Maximize 2X1 + 3X2 - 6X3
subject to:
X1 + 3X2 + 2X3 £ 3,
- 2X2 + X3 £ 1
X1 - X2 + X3 = 2
2X1 + 2X2 - 3X3 = 0
X1 , X2 , X3 ³ 0

The initial tableau is:

BVS X1 X2 X3 S1 S2 RHS
S1132103
S20-21011
?1-11002
?2(2)-3000
Cj23-600

The Push Phase: Bringing X2 into BVS gives the following tableau:

BVS X1 X2 X3 S1 S2 RHS
S1-2013/2103
S220-2011
?20-1/2002
X211-3/2000
Cj-10-3/200

The next variable is X1 to come in:

BVS X1 X2 X3 S1 S2 RHS
S1006105
S200-3/201-1
X110-1/4001
X201(-5/4)00-1
Cj00-7/40 0
R/R----7/5----

Push Further Phase: There is no need for this phase since all Cj's are non-positive.

The Pull Phase: The variable to go out is X2. By row ratio, X3 comes in

BVS X1 X2 X3 S1 S2 RHS
S1024/50101/5
S20-6/50011/5
X11-1/50006/5
X30 -4/51004/5
Cj0-7/5000

This tableau is the optimal one. The optimal solution for decision variables are: X1 = 6/5, X2 = 0, and X3 = 4/5.

Computer Implementation and comparison with other algorithms: For the computerized implementation of this algorithm, some refinements might be needed. For example, in deciding on exchanging the variables, one might consider to total contribution, rather than marginal contribution to the current objective function value. In other words, recall that the choice of smallest non-negative C/R provide the marginal change in the objective function, while maintaining feasibility. However, since we are constructing the C/R for all candidate variables, we may obtain the largest contribution by considering the product Cj (C/R) in our selection rule. The following example illustrates this enhancement in the algorithm:

Example 4: The following problem is attributed to Klee and Minty.

Max 100X1 + 10X2 + X3,
subject to:
X1 £ 1,
20X1 + X2 £ 100,
200X1 + 20X2 + X3 £ 100000,
and X1, X2, X3 ³ 0.

This example is constructed to show that the Simplex method is exponential in its computational complexity. For this example with n= 3, it takes 23 = 8 iterations.

Converting the constraints to equalities, we have: Max 100X1 + 10X2 + X3,
subject to:
X1 + S1 = 1,
20X1 + X2 + S2 = 100,
200X1 + 20X2 + X3 + S3 = 100000,
and X1, X2, X3 ³ 0.

Phase 1: The initial tableau with the two slack variables as its BV is:

BVS X1 X2 X3 S1 S2 S3 RHS C/R1 C/R2 C/R3
S11001001 1 -- --
S22010010100 5 100 --
S3200201001100000 500 5000100000
Cj100101000

Total Contribution Criterion:

Therefore, based on the "total contribution criterion", in our variable selection, variable X3 comes in. Beak any ties arbitrarily.

The Push Further Phase: The candidate variables to enter are X1, X2, and X3 with C/R shown in the above table. Based on the total contribution criterion, the largest contribution to the objective function achieved by bringing X3 in. Therefore, replacing S3 with X3, after pivoting we get:

BVS X1 X2 X3 S1 S2 S3 RHS
S11001001
S22010010100
X3200201001100000
Cj-100-10000-1

This tableau is the optimal one. The optimal solution is: X1 = 100000, X2 = 0, X3 = 0, with the optimal value of 100000.

You may like to install LP Solvers software package on your computer, and checking your computations or for solving larger problems.

Further Readings:

Arsham H., et al., A computer implementation of the push-and-pull algorithm and its computational comparison with LP simplex method, Applied Mathematics and Computation, Vol. 162, No. 4, 1347-1379, 2005.
Arsham H., et al., An algorithm for simplex tableau reduction: The push-to-pull solution strategy, Applied Mathematics and Computation, Vol. 137, No. (2-3), 525-547, 2003.
Arsham H., et al., An algorithm for simplex tableau reduction with numerical comparisons, International Journal of Pure and Applied Mathematics, Vol. 4, No. 1, 57-85, 2003.
Arsham H., A tabular, simplex type algorithm as a teaching aid for general LP models, Mathematical and Computer Modelling, Vol. 12, No. 8, 1051-1056, 1989.
Klee V., and G. Minty, How good is the simplex algorithm, in Inequalities-III, Edited by O. Shisha, Academic Press, 1972, 159-175.

Greater-than-or-equal Constraints Relaxation Method

This solution algorithm is a three-phase simplex-type method, which avoids the use of large numbers known as Big-M's. It combines the primal and dual simplex methods, however it uses parts of objective function as an auxiliary objective function whenever necessary to locate a corner point. In phase 1 some constraints are relaxed to make the origin being feasible (if possible). After solving the relaxed problem using the current solution as the starting point, Phase 2 applies the dual simplex to solve the original problem while Phase 3 applies the primal simplex. Whenever the feasible region is unbounded, in Phase 1 the origin is served as the starting point for Phase 2 to generate a proper corner point by using a "temporary" objective function. Phase 3 restores the original objective function and applies the primal simplex rule to a conclusion. Our initial experimental study with some small size problems indicates that the proposed algorithm is more efficient than both the primal and the dual simplex in terms of the number of iterations, however, further qualification on its assessment is needed.

We start with an LP problem in the following standard form:

Max Z = C . X

subject to
AX £ a
BX ³ b
all X ³ 0,
where b ³ 0, a > 0

Note that the main constraints have separated into two subgroups. A and B are the respective matrices of constraint coefficients, and a and b are the respective RHS vectors (all with appropriate dimensions). Without loss of generality we assume all the RHS elements are non-negative. We will not deal with the trivial cases such as when A=B=0, (no constraints) or a=b=0 (all boundaries pass through the origin). The customary notation is used: Z for the objective, Cj for the cost coefficients, and X for the decision vector. Here, the word constraints means any constraint other than the nonnegativitiy conditions. In this standard form, whenever the RHS is zero, this constraint should be considered as since b is allowed to be 0 but a is not. We depart from the usual convention by separating the constraints into two groups according to £ and ³.

To arrive at this form any general problem some of the following preliminaries may be necessary.

Preliminaries:

- Convert unrestricted variables (if any) to non-negative.
- Make all RHS non-negative.
- Convert equality constraints (if any) into a pair of ³ and £ constraints.
- Remove £ constraints for, which all coefficients are non-positive. This eliminates constraints, which are redundant with the first quadrant constraint.
- The existence of any ³ constraints for, which all coefficients are non- positive and RHS positive, indicates that the problem is infeasible.
- Convert all £ inequality constraints with RHS = 0 into ³ 0. This may avoid degeneracy at the origin.

The following provides an overview of the algorithm's strategy considering the most interesting common case, (a mixture of ³ and £ constraints). This establishes a framework to, which we then extend to complete generality. We proceed as follows:

Phase 1: Relax the ³ constraints and solve the reduced problem with the usual simplex. In most cases we obtain an optimal simplex tableau, i.e. a tableau, which satisfies both optimality and feasibility conditions.
(The discussion of several special cases is deferred for the moment.)

Phase 2: If the solution satisfies all the relaxed constraints, we are done. Otherwise we bring the most "violated" constraint into the tableau and use dual simplex to restore feasibility. This process is repeated until all constraints are satisfied. This step involves several special cases to be discussed after the primary case.

Phase 3: Restore the original objective function (if needed) as follows. Replace the last row in the current tableau to its original values and catch up. Perform the usual simplex. If this is not successful, the problem is unbounded; otherwise the current tableau contains the optimal solution. Extract the optimal solution and multiple solutions (if any).

Special Cases: Three special cases arise in Phase 1, which may require special treatment. If all constraints are ³ and the objective function coefficients satisfy the optimality condition, the origin satisfies the optimality condition but is infeasible. Relax all constraints and start with origin. Some cases may not prove optimal (the relaxed problem has an unbounded feasible region). In Phase 1. the current objective function is changed in a prescribed manner. If all constraints are ³, the origin is not feasible, and if there is any positive Cj we have to change it to 0. This requires restoration of the original objective function, which is done in Phase 3.

Notice that unlike simplex and dual simplex, we focus on the most active constraints rather than carrying all constraints in the initial and all subsequent tableaux. We bring ³ constraints one by one into our tables. This may also reduce computational effort.

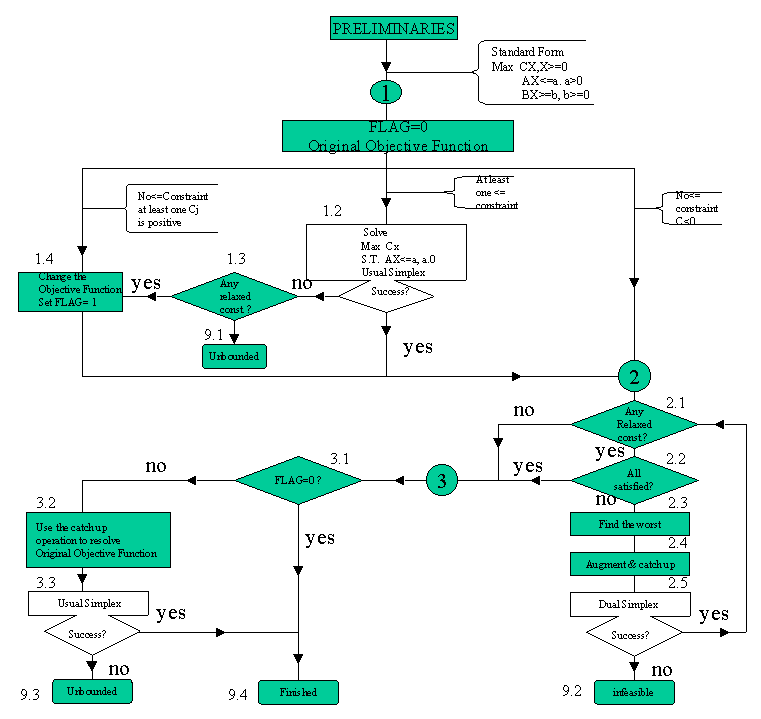
Greater-than-or-equal Constraints Relaxation Method
Click on the image to enlarge it

Detailed Process:

PHASE 1: Recognize three cases as follows:

Step 1.1 Set FLAG=0. This indicates the original objective function is still in use. Check the existence of £ constraints and the signs of the Cjs.
Distinguish there, three possibilities:
a) There is at least one £ constraint. Go to Step 1.2.
b) There are no £ constraints, and no Cj is positive. The origin is the current solution. Go to PHASE 2.
c) There are no £ constraints, and at least one Cj is positive (i.e. A = 0, Cj > 0 at least for one j). Go to Step 1.4.

Step 1.2 From the standard problem relax temporarily all ³ constraints with positive RHS. Solve the sub-problem using the usual Simplex. If successful go to PHASE 2.
Otherwise, go to Step 1.3.

Step 1.3 Are there any ³ constraints?
If yes, go to Step 1.4.
Otherwise go to Step 9.1.

Step 1.4 Change all Cj > 0 elements to 0. Set the FLAG=1. The origin is the starting point. Go to PHASE 2.

Step 9.1 The original problem is unbounded.

PHASE 2: Bring in relaxed constraints (if needed) as follows:

Step 2.1 If there are any remaining relaxed ³ constraint(s),
go to Step 2.2.
Otherwise, go to PHASE 3.

Step 2.2 Does the current optimal solution SATISFY all the still relaxed constraints?
If yes, go to PHASE 3.
Otherwise, go to Step 2.3.

Step 2.3 Find the most violated relaxed constraint. (Substitute the current solution, X, into each constraint and select the constraint with the largest absolute difference between the right and left sides (arbitrary tie-breaker).
Continue with Step 2.4.

Step 2.4 Bring the chosen constraint into the current tableaux .
a) Convert the chosen constraint into a £ constraint and add a slack variable.
b) Use the Gauss Operation to transform the new constraint into the current nonbasic variables. (i.e. Multiply the row for each basic variable by the coefficient of the variable in the new constraint; sum these product rows and subtract this computed row from the new row).
Go to STEP 2.5

Step 2.5 Iterate dual simplex rules to a conclusion:
The dual simplex rule: Use the most negative RHS to select the Pivot Row (if none successful conclusion for Step 2.5). The Pivot Column has a negative coefficient in the pivot row. If a tie results, choose the column with smallest R/R (i.e. row Cj / pivot row element wherever the pivot row element is negative). If there is still a tie, choose one arbitrary. (If there is no positive RR the problem is infeasible i.e. Step 9.2.) Generate the next tableau by using the Gauss pivot operation and repeat the above. For more details on dual simplex rule.
If successful (RHS is nonnegative), go to 2.1.
Otherwise, the problem proves infeasible (No negative element in the outgoing row), go to 9.2.

Step 9.2 The original problem is infeasible.

PHASE 3: Restore the original objective function (if needed) as follows:

Step 3.1 If FLAG=0, go to Step 4.1; otherwise go to Step 3.2.

Step 3.2 Replace the Cj in the current tableau to their original values and catch up.
Go to Step 3.3.

Step 3.3 Perform usual simplex pivoting. If not successful the problem is unbounded go to Step 9.3. Otherwise, go to Step 4.1.

Step 9.3 The original problem is unbounded.

Step 9.4 FINISHED. The current tableau contains the optimal solution. Extract the optimal solution and multiple solutions (if any, i.e. whenever the number of Cj=0 in the final tableau exceeds the number of basic variables). In order to perform the usual postoptimality analysis we can augment the optimal tableau, whenever there are some unused constraints, to obtain the usual final tableau. This can be done easily and efficiently by applying operations a and b of Step 2.4 in turn to each of the nonactive constraints.

Notice that unboundedness can be checked when the selected pivot column has no positive element. Infeasibility is checked whenever the selected pivot row has no negative element.

Numerical Examples

Example 1: The following problem is attributed to Gert Tijssen.

Max -X1 - 4X2 - 2X3,
subject to:
X1 - X2 + X3 = 0,
-X2 + 4X3 = 1,
and X1, X2, X3 ³ 0.

Converting the equality constraints to inequality constraints, we have:

Max -X1 - 4X2 - 2X3,
subject to:
X1 - X2 + X3 £ 0,
-X2 + 4X3 £ 1,
X1 - X2 + X3 ³ 0,
-X2 + 4X3 ³ 1,
and X1, X2, X3 ³ 0.

Relaxing all ³ constraints, we have:

Max -X1 - 4X2 - 2X3,
subject to:
X1 - X2 + X3 £ 0,
-X2 + 4X3 £ 1,
and X1, X2, X3 ³ 0.

Phase 1: The initial tableau with the two slack variables as its BV is:

BVS X1 X2 X3 S1 S2 RHS
S11-11100
S20-14011
Cj-1-4-200

The origin is the solution to the relaxed problem.

Phase 2: Bringing in the violated constraint, we have:

BVS X1 X2 X3 S1 S2 S3 RHS
S11-111000
S20-140101
S301-4001-1
Cj-1-4-2000
R/R----1/2----

The variable to go out is S3 and the variable to come in is X3. After pivoting we have:

BVS X1 X2 X3 S1 S2 S3 RHS
S11-3/40101/4-1/4
S20000110
X30-1/4100-1/41/4
Cj-1-9/2000-1/2
R/R--6--------

The variable to go out is S1 and the variable to come in is X2. After pivoting we have:

BVS X1 X2 X3 S1 S2 S3 RHS
X2-4/310-4/30-1/31/3
S20000110
X3-1/301-1/30-1/31/3
Cj-700-60-2

This is the end of Phase 2. The optimal solution for this tableau is X1 = 0, X2 = 1/3, X3 = 1/3, which satisfies all the constraints. Therefore, it must be the optimal solution to the problem. Notice that since all constraints are in equality form, all slack/surplus variables are all equal to zero, as expected. The optimal value, which is found by plugging the optimal decision into the original objective function, we get the optimal value = -2.

Example 2: The following problem is attributed to Andreas Enge, and Peter Huhn.

Maximize 3X1 + X2 - 4X3
subject to:
X1 + X2 - X3 = 1,
X2 ³ 2,
X1 ³ 0

Converting the equality constraints to inequality constraints, we have:

Maximize 3X1 + X2 - 4X3
subject to:
X1 + X2 - X3 £ 1,
X1 + X2 - X3 ³ 1,
X2 ³ 2,
X1 ³ 0

Relaxing all ³ constraints, we have:

Maximize 3X1 + X2 - 4X3
subject to:
X1 + X2 - X3 £ 1,

Phase 1: The initial tableau with the one slack variable as its BV is:

BVS X1 X2 X3 S1 RHS
S111-111
Cj31-40

The variable to come in is X1, after pivoting we have:

BVS X1 X2 X3 S1 RHS
X111-111
Cj0-2-1-3

The optimal solution is X1 = 1, X2 = 0, X3 = 0. This solution does not satisfy the constraint X2 ³ 2.

Phase 2: Bringing in the violated constraint, we have:

BVS X1 X2 X3 S1 S2 RHS
X111-1101
S20-1001-2
Cj0-2-1-30
R/R--2---- --

The variable to go out is S2, and the variable to come in is X2. After pivoting, we have:

BVS X1 X2 X3 S1 S2 RHS
X110-111-1
X20100-12
Cj00-1-3-2
R/R----1-- --

The variable to go out is X1, and the variable to come in is X3. After pivoting, we have:

BVS X1 X2 X3 S1 S2 RHS
X3-101-1-11
X20100-12
Cj-100-4-3

The optimal solution for the relaxed problem is X1 = 0, X2 = 2, X3 = 1. This solution satisfies all the constraints, therefore, it must be the optimal solution to the original problem.

Example 3:

Max -X1 + 2X2
subject to:
X1 + X2 ³ 2,
-X1 + X2 ³ 1,
X2 £ 3,
and X1, X2 ³ 0.

Relaxing the ³ constraints, the initial tableau is:

BVS X1 X2 S3 RHS C/R
S301133/1
Cj-1200

The variable to come in is X2, after pivoting we have:

BVS X1 X2 S3 RHS
X20113
Cj-10-2

The optimal solution for the relaxed problem is X1 = 0, X2 = 3. The solution satisfies all the constraints, therefore, it must be the optimal solution to the original problem.

Further Reading:

Arsham H., Affine geometric method for linear programs, Journal of Scientific Computing, Vol. 12, No. 3, 289-303, 1997.

Which Solution Algorithm Is the Best?

You may ask "which algorithm is the easiest one?" The answer is that no algorithm is the most efficient to solve all LP problems. The numerical examples in this Web site are solved by almost all algorithms, to show that some solution algorithms do better than others for a specific problem. Therefore, it is not possible to order any set of solution algorithms in terms of their efficiency for all types of LP problems. The following is only a general guideline, which may help you to decide, which algorithm(s) to use for your LP problem. As you've already noticed from the above numerical examples, the "easiest one" depends on Number of Decision Variables, Number of Constraints, and Type of Constraints.

Further Readings:

Klee V., and G. Minty, How good is the simplex algorithm, in Inequalities-III, Edited by O. Shisha, Academic Press, 1972, 159-175.

Goal-Seeking Problems

In most real-life situations the decision maker may not be interested in optimization but wishes to achieve a certain value for the objective function. Most managers are satisfied with a "good enough" solution. This problem is referred to "satisfying" the "goal-seeking" problem.

Some parts of the reason business manager overestimate the importance of optimal strategy is that organizations often use indicators as "proxies" for satisfying their immediate needs. Most managers pay attention to indicators, such as profit, cash flow, share price etc., to indicate survival than as a goal for optimization.

To solve the goal-seeking problem one must first add the goal as part of the constraint set. To convert the goal seeking problem to an optimization problem one must create a dummy objective function. It could be a linear combination of the sub-set of decision variables. If you maximize this objective function, you will get a feasible solution (if one exists). If you minimize it, you will maybe get another one (usually at the other "side" of the feasible region). You could optimize with different objective functions.

Another approach is to use "Goal Programming" models, which deal precisely with problems of constraint satisfaction without necessarily having a single objective. Basically, they look at measures of constraint violation, and try to minimize these. You can formulate and solve goal programming models in ordinary LP, using ordinary LP solution codes.

In the artificial-free solution algorithms, one may use a zero dummy objective function but not in some software packages such as Lindo. In using software packages one may maximize or minimize any variable as an objective function.

Numerical Example

Consider Example 1 in the Initialization of the Simplex Method section of a companion site to this site. Suppose instead of maximizing, we now wish to achieve a goal of 4. That is,

Goal: -X1 + 2X2 = 4
subject to:
X1 + X2 ³ 2,
-X1 + X2 ³ 1,
X2 £ 3,
and X1, X2 ³ 0.

Adding this goal to the constraint set, and converting the constraints into equality form, we have:

X1 + X2 - S1 = 2, -X1 + X2 - S2 = 1, X2 + S3 = 3, and
X1, X2, S1, S2, S3 ³ 0.

The initial tableau for this problem, with dummy objective function of 0, is:

BVS X1 X2 S1 S2 S3 RHS C/R
? (1)1-1002 2/1
?-110-101-1/1
?010013 ---
? -120004-4/1
Cj000000

X1 comes in. The next tableau is:

BVS X1 X2 S1 S2 S3 RHS C/R
X111-10022/1
?0(2)-1-1033/2
?0100133/1
?03-10066/3
Cj000000

Similarly, bringing the other variables in the BV set, we get:

BVS X1 X2 S1 S2 S3 RHS C/R
X110-1/21/201/2-1
X201-1/2-1/203/2-3
?00(1/2)1/213/23
?001/2-3/203/23
Cj000000

The next tableau is:

BVS X1 X2 S1 S2 S3 RHS C/R
X11001122
X2010013---
S10011233
?000(-2)-100
Cj000000

And finally:

BVS X1 X2 S1 S2 S3 RHS
X11000-1/22
X2010013
S10010-3/23
S200011/20
Cj000000

A solution is X1 = 2, X2 = 3, S1 = 3, S2 = 0, and S3 = 0.

How to Solve ILP by LP Solvers? Cutting Plane Method

Suppose that we wish to solve the following Integer LP problem:

Max 14X1 + 30 X2
subject to:
7X1 + 16 X2 £ 52
3X1 -2X2 £ 9
and both decision variables must be non-negative integers.

The first step is to relax (i.e., ignore) the integrality condition and solve this problem as an LP. The result is X1 = 4, and X2 =3/2. This solution is not feasible for the ILP problem. The customary practical approach is to round the solution to the near integers, that is, X1 = 4, X2 = 1, or X1 = 4, X2 = 2. Unfortunately, none of these are even feasible for the ILP. Even, if any one of them were feasible, we are not sure that it is optimal. Therefore, an effective approach, which guarantee an optimal solution (if one exists) must be used. An effective approach is known as "The Cutting-Plane Method", which cuts off the feasible region to exclude the obtained non-integer variables one-by-one.

In the application of cutting plane method, initially, we ignore the integer condition by solving the problem as an LP problem, if the solution satisfies the integrality condition(s), we are done. Otherwise, we add a new constraint to exclude (to cut-off) this solution while including all the original feasible solutions. The following small numerical example illustrates the process.

Max 3X1 + 5X2
subject to:
X1 + 8/5X2 £ 4
both decision variables must be non-negative integers.

The first step is to make all coefficients in the problem integer, if necessary. Therefore, the equivalent ILP problem to this problem is:

Max 3X1 + 5X2
subject to:
5X1 + 8X2 £ 20
both decision variables must be non-negative integers.

Using the simplex method, we get the following final tableau:

BVS X1 X2 S1 RHS
X25/811/85/2
Cj-1/80-5/8

Therefore, X1 = 0, X2 = 5/2. This solution is not integer, and if we round this solution, both results are feasible but not optimal, as we will find later. Therefore, we must introduce a cut.

In the final table, consider the row, which the RHS violates the integrality condition. Break any ties, arbitrarily. In this numerical example, we have to consider the first row (i.e., the only row) in the above table. Find out "the rounding-it down fraction" for each entries in that row. That is, the absolute-value of the fractional-number needed to round-down each entry in that row. Construct the cut. The cut is always a constraint of ³ form with all non-negative coefficients, including the RHS. For this problem, the cut is 5/8X1 + 1/8S1 ³ 1/2. Following the steps described in the Initialization of the Simplex Method with this added new constraint, we get the final tableau:

BVS X1 X2 S1 S2 RHS
X201012
X1101/5-8/54/5
Cj00-3/5-1/5

Still, the solution is not satisfactory. Introducing another cut: 1/5S1 + 2/5S2 ³ 4/5, we obtain the following final tableau.

BVS X1 X2 S1 S2 S3 RHS
X201-1/205/40
X11010-44
S2001/21-5/22
Cj00-1/20-1/2

Therefore, the optimal solution is: X1 = 4, X2 = 0, with optimal value of 12.

The following sites enable you to practice the LP pivoting without having to do the arithmetic!
The Pivot Tool , tutOR, The Simplex Place, Simplex Machine, and LP-Explorer.

A selection of:

|Academic Info Association for Facilities Engineering (AFE)| BUBL Catalogue| Business Majors| Decision Sciences Institute| Education World| Investigación Operativa|

|Management| Mathematics Resources| MathForum: Engineering| NEEDS| Operations Management| OR Resources| Penn State U.| Portuguesa de Investigação Operacional|

Search Engines Directory
| AltaVista| AOL| Excite| HotBot| Looksmart| Lycos| MSN| Netscape| NetFirst| OpenDirectory| OpenHere| Webcrawler| Yahoo|

|Scout Report for Business & Economics |Virtual Library|

The Copyright Statement: The fair use, according to the 1996 Fair Use Guidelines for Educational Multimedia, of materials presented on this Web site is permitted for non-commercial and classroom purposes only.
This site may be mirrored intact (including these notices), on any server with public access, and linked to other Web pages. All files are available at http://www.mirrorservice.org/sites/home.ubalt.edu/ntsbarsh/Business-stat for mirroring.

Kindly e-mail me your comments, suggestions, and concerns. Thank you.

Professor Hossein Arsham   

This site was launched on 2/25/1994, and its intellectual materials have been thoroughly revised on a yearly basis. The current version is the 8th Edition. All external links are checked once a month.

Back to:

Dr Arsham's Home Page

EOF: © 1994-2003.