-Capital Budgeting with Risk

The capital budgeting model considers risk by computing the statistical variance (and standard deviation) of each project and either minimizing the portfolio variance or placing a constraint on portfolio variance. When risk is considered, the initial investment, net income, and salvage value of each project are assumed to be random variables with specified mean values and standard deviations. For this analysis the life of a project is not a random variable, but is a fixed value. 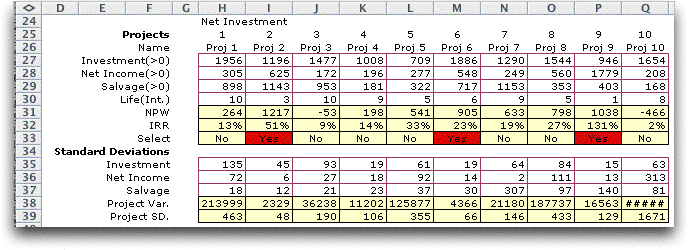Although it is sometimes convenient to assume Normal distributions for the random variables, it is not necessary for these results. The data for the projects in an example problem are shown in the table below. For the example we assume that all random variables are statistically independent.

The mean values for the investment, net income and salvage are given for the example in rows 27 through 29 and the corresponding standard deviations are given in rows 35 through 37. The project lives are in row 30.

It is easily shown using basic definitions that the weighted sum of independent random variables is a random variable whose mean and variance can be calculated as below.

Since the present worth values are computed as a weighted sum of the components, the mean and variance for the NPW for each project are computed as below.

Row 31 in the table above holds the values of the mean NPW for each project and row 38 holds the values of the variance for each project. The variance for Project 10 is too great to display with the current column width. Row 39 is the square root of row 38, and holds the standard deviations of the projects.

Using the same principles, the mean and variance of the portfolio can be expressed as functions of the decision variables.

The portfolio variance is a nonlinear function of the decision variables, but when the values or the decision variables are restricted to 0 and 1, the variance can be expressed as a linear function. We use the linear expression in models with the 0-1 restriction. This allows models to be solved using linear-integer programming rather than nonlinear-integer programming. The latter is much less reliable than the former.

Math Programming Model

With these definitions, several optimization models are possible depending on the goal of the analyst and the constraints that are included. We can maximize the NPW while placing an upper bound constraint on the variance, we can minimize the variance while placing a lower bound constraint on the NPW, or we can minimize the initial investment while placing constraints on both the variance and the NPW. In each case we assume that the model includes a budget constraint. The options are set on the Capital Budgeting dialog.

The figure below shows the three models when the selection variables are limited to 0 or 1, representing not select or select. Since all the models are linear, integer-linear programming can be used to find the optimum portfolio of projects.

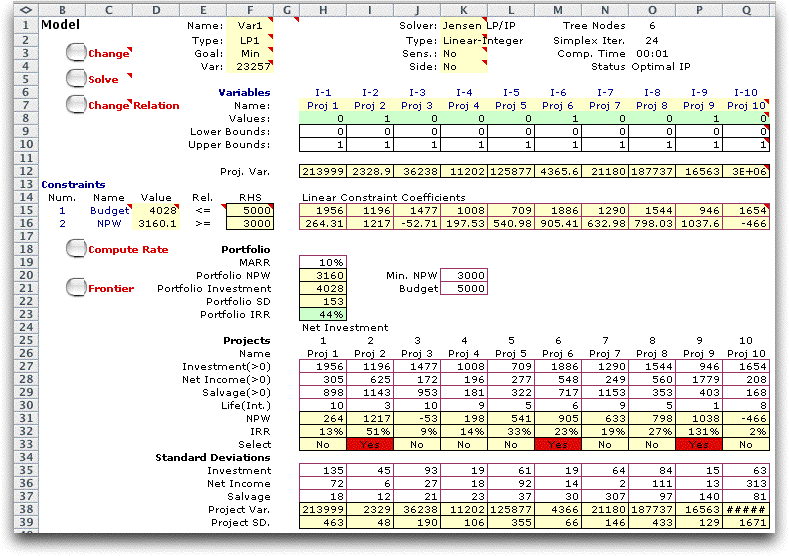
The worksheet below shows the minimum variance solution for the example. Cells K21 and K22 are provided to hold the minimum NPW and the Budget respectively. These are controlled by the analyst. Of course when the cells are changed the model must be solved to obtain the new solution.

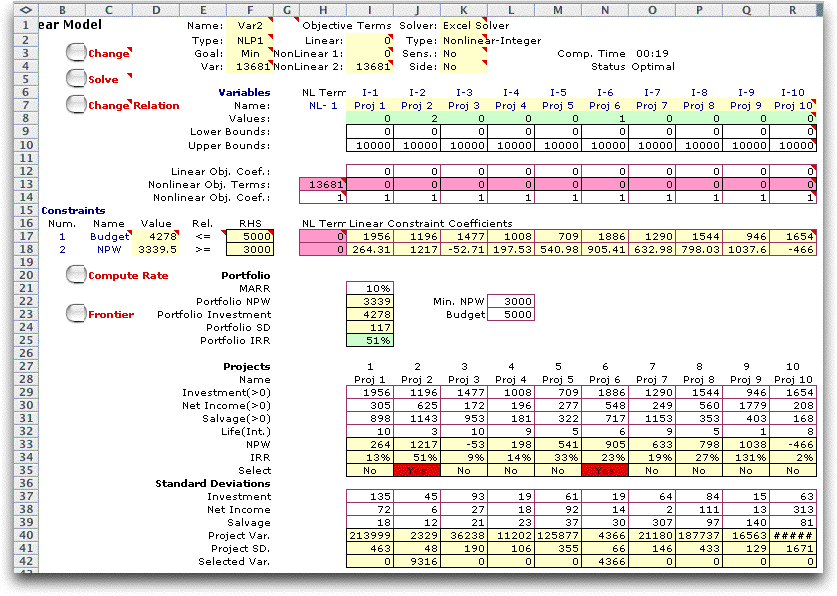
When variables are allowed to assume values greater than 1 or the integrality restriction is dropped, the optimization model is nonlinear.

The add-in creates the nonlinear-integer model below when the variables are not restricted to binary values. Cell H13 holds a nonlinear term than is the sum of the variance multiplied by the values of the squared number of projects. The optimum selects two of project 2 and one of project 6. Since the variable values are squared, the solution tends to have solutions with several selected projects rather than several copies of the same project. In the example two units of project 2 are selected because it has such a low variance. The model is both nonlinear and integer. The Excel Solver can solve such models, but the performance is much reduced in comparison to a linear-integer model. If the Solver fails to find a feasible solution, it is always a good idea to try alternative initial solutions. We have used the variable values 1/n with some success.

By sequentially solving this problem with different limits on the NPW constraint, the analyst can construct a set of solutions each with the minimum variance for the obtained value of the NPW. We illustrate with the model having binary variables. We set the budget for the example problem to be very large and not constraining and solve the problem for increasing limits on the NPW. A set of solutions is obtained. 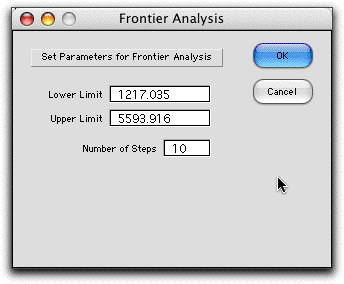Plotting the solutions on a chart with NPW and variance as the axes, one obtains what is called the efficient frontier of solutions. To find the efficient frontier click the Frontier button on the worksheet. The program finds the lower limit by setting the NPW constraint limit to 0 and solving the model. The lower limit obtained is the NPW of the minimum variance portfolio. The upper limit is the sum of the positive project NPW values. To make a more refined search, these limits may be changed. The Number of Steps entry specifies how many individual problems are solved. The NPW range is divided into this number of equal intervals.

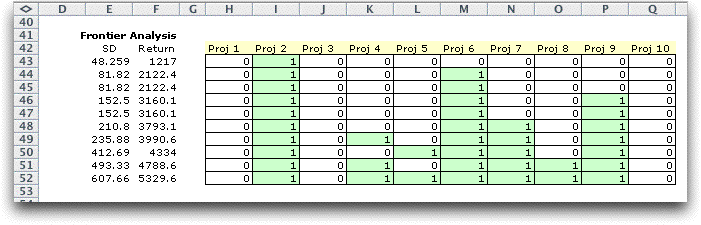
The model being solved is a linear-integer programming model. It is solved 11 times. Excluding the last value for which the program cannot find a feasible solution, we obtain the solutions in the table below. Green cells indicate nonzero values.

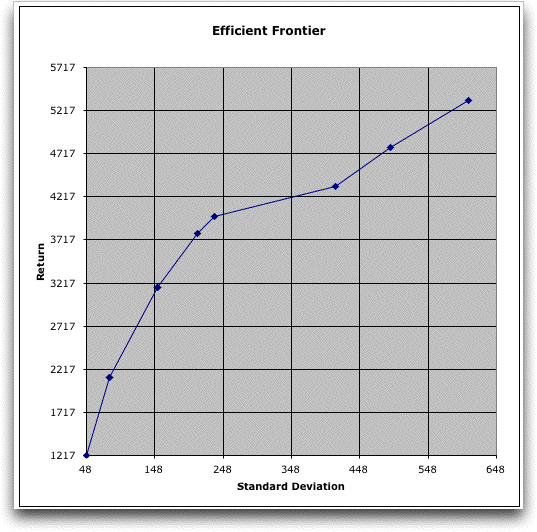
A graph of the efficient frontier appears immediately below the table. We connect the individual points with straight lines, but since a finite number of solutions are generated this is only an approximatin of the frontier. If the entire frontier were available, any solution not on the efficient frontier is dominated by some solution on the frontier. There are portfolios with values that appear below the frontier, but none that are above. With continuous decision variables the frontier has a concave shape. With discrete variables, the shape may not be concave. Since the NPW values are chosen with fixed size steps, the curve may not show all solutions on the frontier. Also different values of NPW may yield the same solution.

The same solutions will be found by maximizing the NPW with a constraint on the maximum variance, however the automatic feature of the program is only available when minimizing the variance.

It is conceivable that projects are not statistically independent. The returns of dependent projects are related through a correlation matrix. To form a model with correlation, click the appropriate checkbox in the dialog.

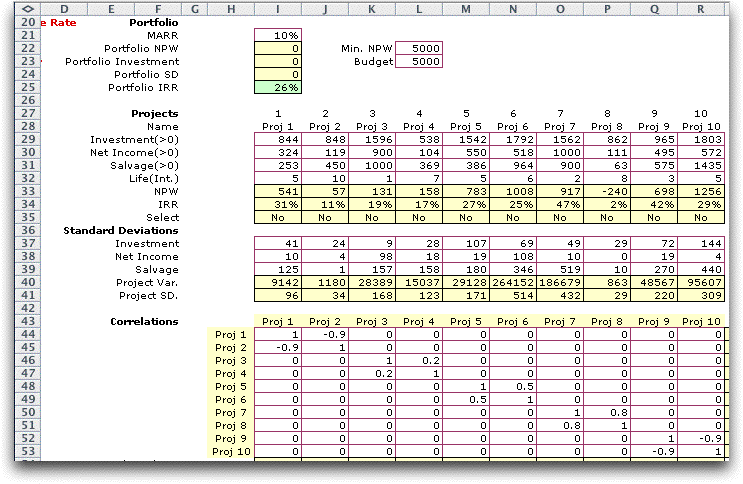
The data for a correlated model is shown below. A correlation matrix is included below the return and variability data. A valid matrix has 1's on the diagonal, is symmetric and has numbers between -1 and +1 on the off-diagonals. The resultant matrix must be positive definite.

This matrix is filled by the modeler with information concerning the correlation between projects. We have illustrated the situation by providing nonzero correlation coefficients between pairs of projects. Note that we have included a large negative correlation coefficient between the pairs (1, 2) and (9, 10). For selected projects with negative correlation, the statistical variability tends to cancel out.

The variance of the portfolio is a nonlinear function of the decision variables as shown below. The portfolio variance function is used in the several model formulations when correlation is part of the model. A related result is used extensively for Markowitz portfolios considered on the next page.

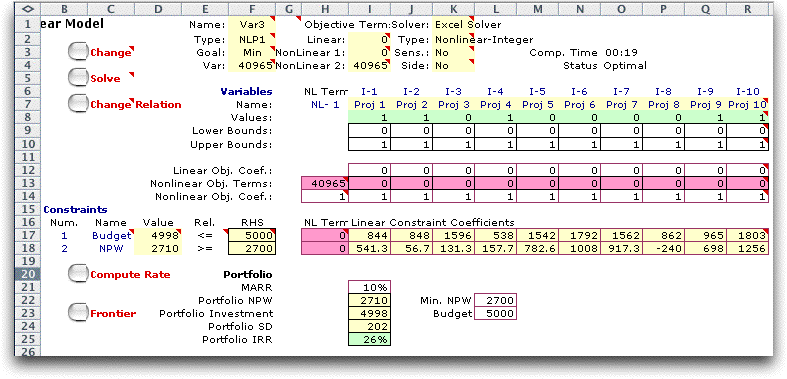
The solution for the example is shown below. Note that the two pairs of negatively correlated variables are both used in the solution. Actually the solution shown was obtained with some difficulty. The Solver often does not find exact solutions for nonlinear-integer programming problems.