|
|
 |
Queuing
Add-in
|
 |
-
Non-Markovian Queues |
 |
|
The add-in computes approximate values for
the steady-state measures when the arrival or service processes
are not required to have exponential distributions.
To add a non-Markovian Queuing model
on the worksheet, place the cursor at a cell where the model
is to be described and select Add NonMarkov from the
menu. The dialog box below allows entry of the parameters of
the model. This model does not require the interarrival and
service distributions to have exponential distributions. Rather,
the model requires the specification of the coefficients of
variation (COV) of the arrival and service processes. The COV
for arrivals is the standard deviation for time between arrivals
divided by the mean time between arrivals . For an exponential
distribution the COV is 1. Distributions with less variability
than the exponential have COV < 1, while distributions with
more variability have COV > 1. The service process COV is
the standard deviation of the service time divided by the mean
service time.
|
 |
Example: An order picking process
|
An order picking process in a warehouse gets calls
for service at an average rate of 8.5 per hour. The
average time to fill the order is 0.1 hours. For analysis
purposes assume both times are exponentially distributed.
Analyzing the system as an M/M/1 queue, the average
time in the queue is 0.5667 hours. An opportunity arises
to reduce the variability of the process for filling
orders. The inventory manager wonders if the change
is worth the cost.
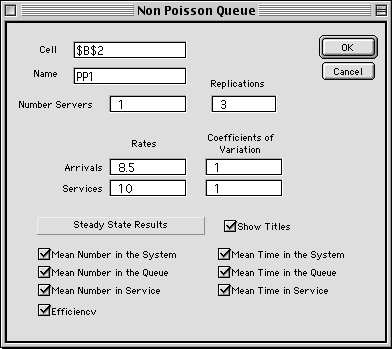
To analyze this problem we select
the NonMarkov option from the menu. The dialog below
defines the parameters of the model. The name, arrival
rate, service rate and number of channels are entered
in the appropriate boxes. The approximation does not
apply to finite queues or finite populations, so these
options are not present. If the replication entry is
greater than 1, the number entered determines the number
of Queuing models put on the worksheet. We illustrate
the presentation of three replications below.
|
|
 |
The check boxes on the dialog determine
optional presentation of the steady state results. Checking
the Show Titles box causes titles to be added to
the worksheet. When defining a series of Queuing models
in sequential cells, it is useful to show the titles for
the first model, and then skip the titles for the remaining
models.
The set of results for the Non-Markovian
case is smaller than those available for Poisson queues.
This is partially due to the restriction against finite
queues and finite populations, making some results not relevant.
The approximations used do not allow the computation of
state probabilities.
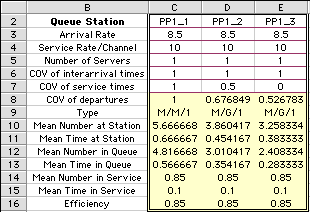
The results for three replications of the Queuing model
are shown below. When the models were created on the worksheet
all had the default parameters shown for PP1_1. To illustrate
the effect of reducing the variability in the service times,
we set the COV to 0.5 in the second model and 0 in the third
(no variability). In general the numbers and time in the
queue decrease as variability decreases. Note that with
COV of 1, the distribution is actually Markovian (Poisson
process). Thus we see an M in the type designation when
the COV is 1.
It is clear from the results that reducing variability
in the service process causes decreased time in the queue.
The mean time in service does not change because that is
fixed by the data and unaffected by the variability.
|
 |
Using Reduced Variability to Obtain more Throughput
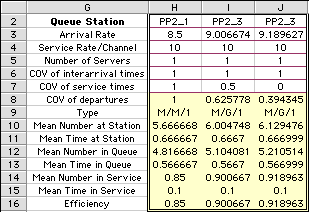
| We wonder whether the benefits of the reduced variability
could be used to obtain more throughput, rather than
reduced queues. That is, we want to increase the arrival
rate in the second two systems to obtain a time in the
queue equal to 0.567. This is indeed possible as shown
in the analysis below. Note that for the systems in
columns I and J, the arrival rates have been increased
substantially while the time in the queue remains at
0.567. |
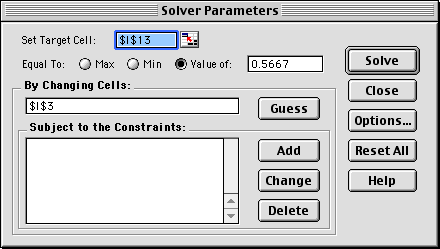
This analysis was performed using the Excel
Solver, called with the Solver command on the Tools menu
of Excel. The Solver dialog shown below is set up to obtain
the solution in column I above. The target cell,
I13, holds the mean time in the queue. The changing cell,
the cell I3, holds the arrival rate. We have asked Solver
to find the value of the arrival rate that gives a mean
queue time of 0.5667. When performing the analysis it was
necessary to give an initial value larger than the ultimate
solution of 9.006. With a smaller initial value, Solver
tried arrival rates greater than 10 and the procedure stopped
because the system is unstable for arrival rates greater
than 10.
|
 |
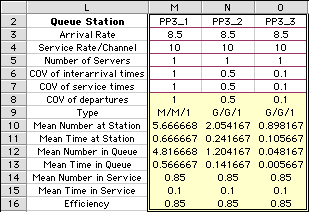
Reducing Variability of Both Arrival and Service Processes
Reducing the variability of both the interarrival times
and service times further reduces the time in the queue
as shown below. The results of column N show that by cutting
the COV to 0.5 reduces the queue time to 1/4 of its value
with Poisson processes. Reducing the COV's for both processes
to 1/10 the original value reduces the queue time to 1/100
of its former value.
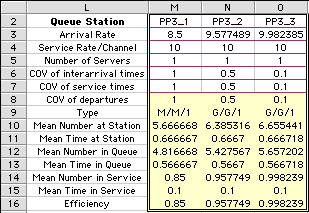
Again we investigate the possibility of increased
throughput while keeping queue time as a constant. We used
Solver as previously described to obtain the results below.
The arrival rate for the third case is at almost the theoretical
maximum of 10.
When both COV are equal to 1 the system can
be analyzed with no approximation using the Poisson queueing
formulas. The formulas used by the Non-Markovian analysis
are also accurate for M/G/1 systems. For all other systems,
the results are approximate.
|
|



